0 问题：
如表1，假设是某项目路段预测交通量，给出了特征年的交通量，如何计算中间某年的交通量，比如2023年的交通量。

表1 某项目特征年预测交通量

特征年	2017年	2020年	2025年	2036年
交通量	28887	52999	93224	122440

1 方法一：
内插法又称插值法。根据未知函数f(x)在某区间内若干点的函数值，作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x)，进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值，这种方法，称为内插法。按特定函数的性质分，有线性内插、非线性内插等；按引数(自变量)个数分，有单内插、双内插和三内插等。[1]
当然，我们会选择最简单的线性内插，公式如下：

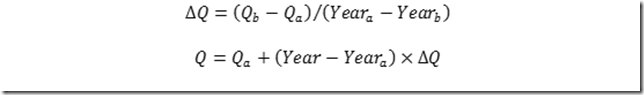
例如，2023年的交通量=52999+（2023-2020）×（93224-52999）/(2025-2020)。
2 方法二：
年均增长率法，统计学相关概念。在人口预测中常见，指一定年限内，平均每年增长的速度。[2]
公式如下：

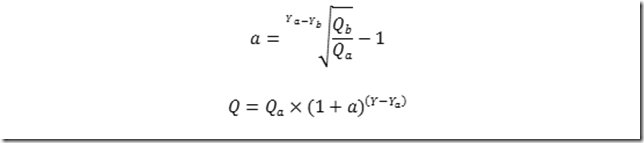
例如，2020年到2025年的年均增长率=（93224/52999）^（1/（2025-2020））
3 讨论：
各特征年间的平均差值和平均增长率如表2所示。

表2 各特征年平均差值和平均增长率

特征年	2017	2020	2025	2036
交通量Q	28887	52999	93224	122440
平均差值△Q		8038	8045	2656
平均增长率a		22%	12%	3%

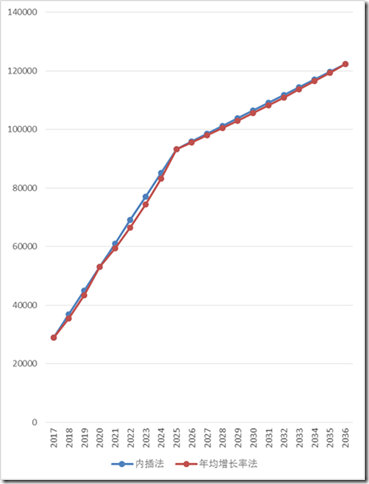
图1 各年交通量折线图

可以看出，
（1）由线性内插法和年均增长率法计算得到的各年交通量并不相等，但是因为有特征年的约束，其差别不是太大。
（2）年均增长率法计算结果前期增长慢后期增长快。
（3）把由内插法计算得到的各年交通量反算一个增长率，以及把由年增长率法计算得到的各年交通量反算一个差值，综合起来得到图2。

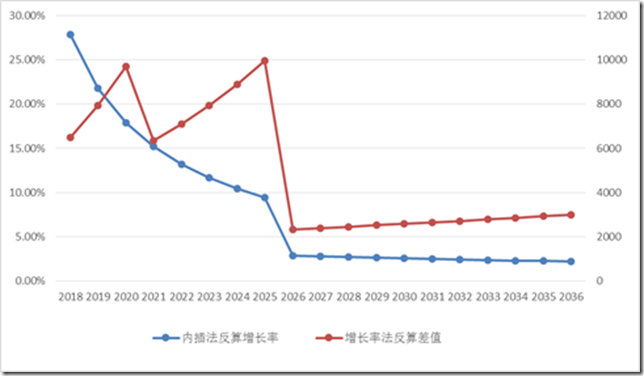
图2 反算结果

（4）交通量预测时常用的相关系数法，也即采用GDP增长率等社会发展参数估计交通量增长率。那么每年的GDP增长率是不同的，则每年的交通量增长率也不同。一般规律是GDP增长率逐年下降，与内插法反算出来的增长率规律相同。
（5）那么说内插法的计算结果更符合现实的规律？

---

[1]内插法： http://baike.baidu.com/view/37696.htm?fr=aladdin
[2]年均增长率: http://baike.baidu.com/view/2102486.htm